583. Delete Operation for Two Strings

Problem 

Given two strings word1 and word2, return the minimum number of steps required 
to make word1 and word2 the same.
In one step, you can delete exactly one character in either string.


Example 1:
Input: word1 = "sea", word2 = "eat"
Output: 2
Explanation: You need one step to make "sea" to "ea" and another step to make "eat" to "ea".

Example 2:
Input: word1 = "leetcode", word2 = "etco"
Output: 4

Constraints:
1 <= word1.length, word2.length <= 500
word1 and word2 consist of only lowercase English letters.

Approach

Tóm tắt đề bài: Cho 2 chuỗi string w1, w2. Mỗi lần ta có thể xoá bớt 1 kí tự bất kì của 1 trong 2 chuỗi.
Tìm số thao tác xoá ít nhất để chuỗi w1 = w2

image 1 Đọc kĩ đề bài, mỗi lượt ta chỉ có thể có 2 action:

  • Xoá một kí tự
  • Không làm gì cả

Gọi i, j lần lượt là pointer index của w1 và w2
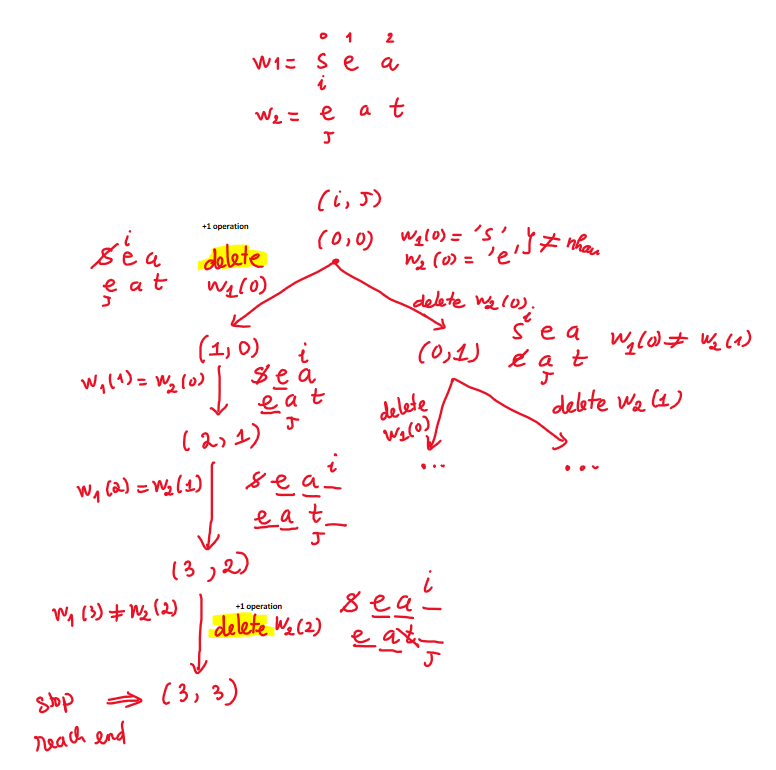
Ta lần lượt so sánh các kĩ tự w1(i) và w2(j) xem chúng có bằng nhau hay là không? Từ đó lựa chọn action tương ứng (có thể xem hình 1)
Như hình 1, w1(0) != w2(0) nên ta có 2 lựa chọn:

  • Xoá kí tự w1(0). Ta so sánh các kí tự còn lại w1 = _ea và w2 = eat
  • Xoá kí tự w2(0). Ta so sánh các kí tự còn lại w1 = sea và w2 = _at

Tương tự như vậy cho đến khi i, j tiến tới hết chỗi (i = w1.length và j = w2.length)

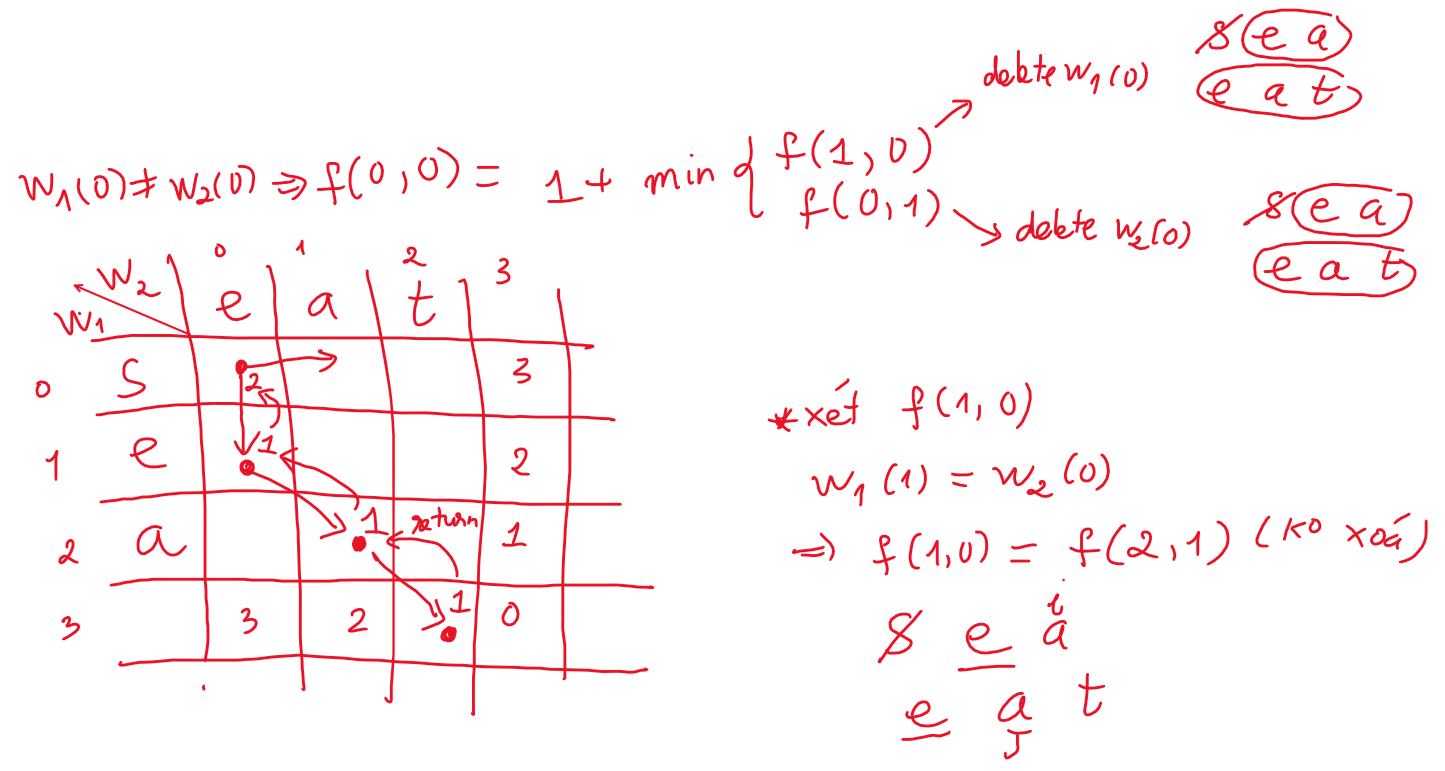image 2 Sau khi giải cách đệ quy ở trên, ta có thể mô hình hoá cách đệ quy ở trên bằng table
Với hàm f(i, j) là số operation nhỏ nhất của chuỗi w1[i..end] và w2[j..end]
Và công thức quy hoạch động như hình với 2 trường hợp:

  • w1(i) != w2(j) => f(i, j) = 1 + min(f(i+1, j), f(i, j+1)

  • w1(i) = w2(j) => f(i, j) = f(i+1, j+1)

  • Ngoài ra, vì sao f(0, 3) = 3. Thì ta cần ít nhất 3 thao tác xoá các kí tự s, e, a của w1 = sea để w1 trở thành w2 = _ (empty).
    Tương tự, f(n, j) = m - j (0 <= j <= m) và f(i, m) = n - i (0 <= i <= n) với n = word1.length và m = word2.length

Có thể thấy công thức QHĐ rõ ràng ở phần implementation bên dưới

Implementation

1. Recursion + memorization 

class Solution {
    private String word1;
    private String word2;
    private Map<String, Integer> memo;

    public int minDistance(String word1, String word2) {
        this.word1 = word1;
        this.word2 = word2;
        this.memo = new HashMap<>();

        return dfs(0, 0);
    }

    private int dfs(int i, int j) {
        // base case
        if (i == word1.length() && j == word2.length()) {
            return 0;
        }

        String key = i + "_" + j;
        if (memo.containsKey(key)) {
            return memo.get(key);
        }

        int ans = 0;

        // case: w1(i) = w2(j) => both increase (i,j)
        if (i < word1.length() && j < word2.length()
                && word1.charAt(i) == word2.charAt(j)) {
            ans = dfs(i+1, j+1);
        }
        // case: w1(i) != w2(j)
        else {
            if (i == word1.length()) {
                ans = 1 + dfs(i, j+1); // delete w2(j) => increase j
            } else if (j == word2.length()) {
                ans = 1 + dfs(i+1, j); // delete w1(i) => increase i
            } else {
                // delete w1(i) or delete w2(j)
                ans = 1 + Math.min(dfs(i+1, j), dfs(i, j+1));
            }
        }

        memo.put(key, ans);
        return ans;
    }
}

Dynamic programming 

class Solution {
    public int minDistance(String word1, String word2) {
        int n = word1.length(); int m = word2.length();

        int[][] dp = new int[n+1][m+1];
        dp[n][m] = 0;
        for (int r = 0; r < n; r++) {
            dp[r][m] = n - r;
        }
        for (int c = 0; c < m; c++) {
            dp[n][c] = m - c;
        }

        for (int i = n-1; i >= 0; i--) {
            for (int j = m-1; j >= 0; j--) {
                if (word1.charAt(i) == word2.charAt(j)) {
                    dp[i][j] = dp[i+1][j+1];
                } else {
                    dp[i][j] = 1 + Math.min(dp[i+1][j], dp[i][j+1]);
                }
            }
        }

        return dp[0][0];
    }
}