1877. Minimize Maximum Pair Sum in Array

Problem

The pair sum of a pair (a,b) is equal to a + b. The maximum pair sum is the largest pair sum in a list of pairs.

For example, if we have pairs (1,5), (2,3), and (4,4), the maximum pair sum would be max(1+5, 2+3, 4+4) = max(6, 5, 8) = 8.
Given an array nums of even length n, pair up the elements of nums into n / 2 pairs such that:

Each element of nums is in exactly one pair, and
The maximum pair sum is minimized.
Return the minimized maximum pair sum after optimally pairing up the elements.

 

Example 1:
Input: nums = [3,5,2,3]
Output: 7
Explanation: The elements can be paired up into pairs (3,3) and (5,2).
The maximum pair sum is max(3+3, 5+2) = max(6, 7) = 7.

Example 2:
Input: nums = [3,5,4,2,4,6]
Output: 8
Explanation: The elements can be paired up into pairs (3,5), (4,4), and (6,2).
The maximum pair sum is max(3+5, 4+4, 6+2) = max(8, 8, 8) = 8.
 
Constraints:
n == nums.length
2 <= n <= 105
n is even.
1 <= nums[i] <= 105

Intuition

Tóm tắt đề bài: Có một mảng nums có số lượng phần tử là n chẵn. Từ trong mảng, tiến hành tạo thành các cặp (nums[i], nums[j]) (i != j), ta được n/2 cặp số và tìm max sum trong tất cả cặp số đó. Và có X = 2Cn * 2Cn-2 * 2Cn-4 *...* 2C2 cách tạo cặp từ mảng n phần tử. Từ trong X cách đó, tìm ra max sum bé nhất trong tất cả các cách
Nghĩ đến phương pháp tham lam, do đề bài cần tìm max sum nhỏ nhất trong tất cả các cách, nên để cho cân bằng mình sẽ ghép cứ một số lớn nhất và một số nhỏ nhất là một cặp, một số lớn thứ 2 với một số nhỏ thứ 2 là 1 cặp,… Và vì sao cách này lại hiệu quả thì xem phần chứng minh bên dưới
Bài này, mặc dù dự đoán cách giải => submit AC đáp án, nhưng để chứng minh cách giải đúng thì lại khó hơn các bài khác :))
Approach
Sort mảng, dùng 2 pointer left, right chạy từ đầu mảng và cuối mảng vào trung tâm để tạo thành các cặp và tìm max sum
Tại sao dùng cách trên ta sẽ tìm được minimized maximum pair sum trong tất cả các cách ghép cặp?
- Điều quan trọng trong đề bài ở chỗ minimized
- Giả sử: nums = [a, b, c, d, e, f] đã được sort tăng dần
- Ta có: a < b < c < d < e < f
- Ta liền tạo thành các cặp (a, f) (b, e) (c, d) và tìm max sum ở 3 cặp này thì sẽ được đáp án minimized maximum pair sum
- Và giả sử cặp cặp đó chính là (b, e)
- Do mình có nhiều cách ghép cặp, mình cũng thể ghép thành 1 cách như này: (a, c), (d, e), (b, f). Thì ra rõ ràng thấy: nếu cặp (b, f) là cặp lớn nhất ở trong cách xếp này thì (b, f) không phải max sum nhỏ nhất trong các cách vì (b+f) > (b+e) (do e < f), cặp (d, e) cũng không phải đáp án vì (d+e) > (b+e) (do d > b). Còn cặp (a, c) là cặp nhỏ nhất trong 3 cặp (a, c), (d, e), (b, f), không thể là max sum trong cách này nên ta không xét
- => Vì vậy, ta ưu tiên ghép các cặp đối xứng nhau sau khi mảng đã sắp xếp tăng dần

Sau khi mình tự giải và tự giải thích theo luồng suy nghĩ, thì có đọc được một số comment ở phần solution này: https://leetcode.com/problems/minimize-maximum-pair-sum-in-array/editorial/ khá hay, có thể đọc để hiểu hơn cách chứng minh (có cách tương tự của mình)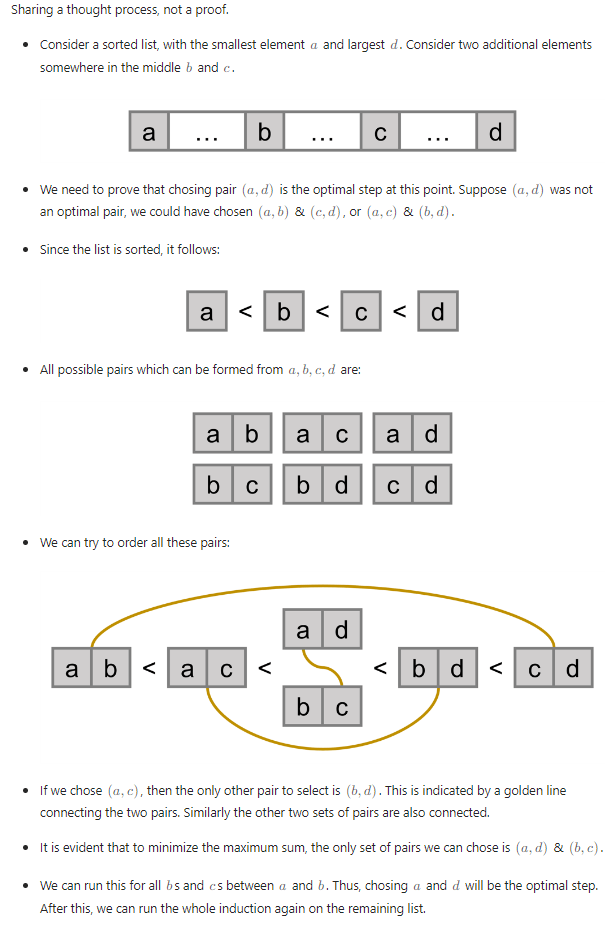

Implementation

class Solution {
    public int minPairSum(int[] nums) {
        int n = nums.length;
        int l = 0; int r = n-1;

        Arrays.sort(nums);

        // n is even so not need l <= r
        int maxSum = Integer.MIN_VALUE;
        while (l < r) {
            maxSum = Math.max(maxSum, nums[l] + nums[r]);
            l++; r--;
        }

        return maxSum;
    }
}

1877. Minimize Maximum Pair Sum in Array

Problem

Intuition

Approach

Implementation